Continue with the previous article.
The following rules in texts are exactly the same to traditional chess rules, and the diagrams are the implementations of traditional chess rules on the Dot.
On the diagrams, little black dots on the squares mark the piece’s destinations. Lines between piece and dots mark all routes from piece to its destinations.
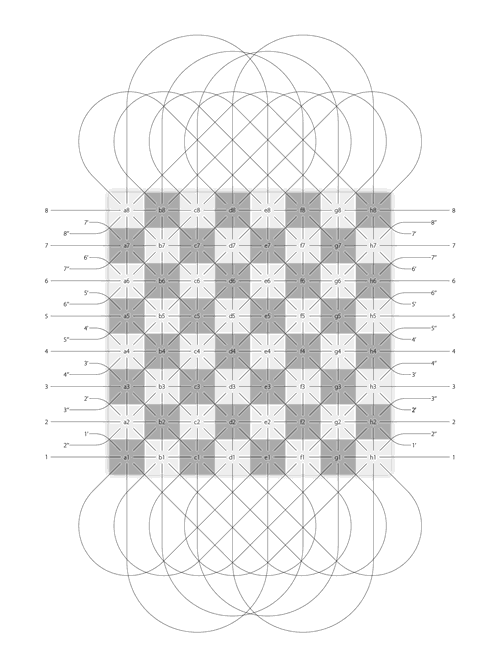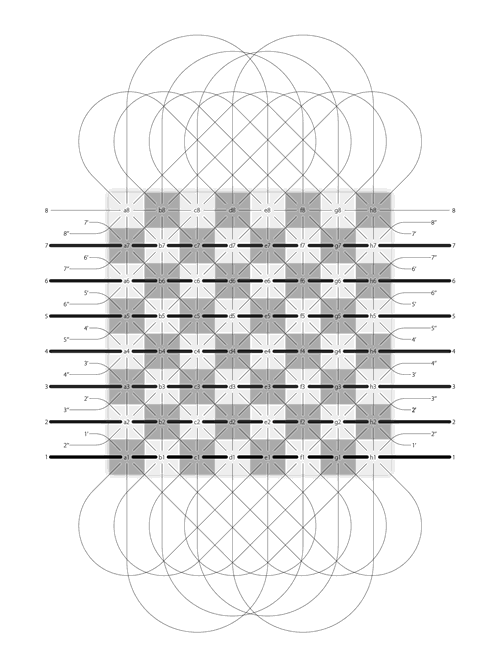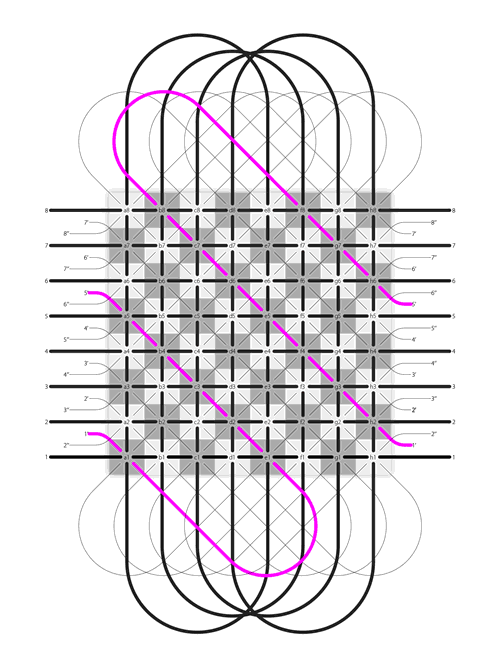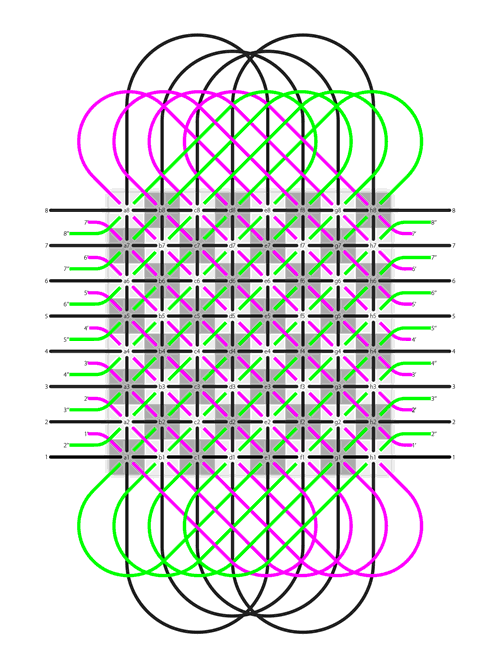
Rook: The rook can move any number of squares along any rank (latitude) or file (longitude), but may not leap over other pieces. It moves the same way when capture an opponent’s piece.
 |
| Rook's move and capture on the Dot |
Bishop: The bishop can move any number of squares along any diagonal, but may not leap over other pieces. It moves the same way when capture an opponent’s piece.
 |
| Bishop's move and capture on the Dot |
Queen: The queen can move any number of squares along any rank (latitude), file (longitude) or diagonal, but may not leap over other pieces. It moves the same way when capture an opponent’s piece.
 |
| Queen's move and capture on the Dot |
King: The king can move only one square along any rank (latitude), file (longitude) or diagonal. It moves the same way when capture an opponent’s piece.
 |
| King's move and capture on the Dot |
Knight: The knight can move to any of the closest squares that are not on the same rank, file, or diagonal, thus the move forms an “L-shape”: two squares along rank (latitude) and one square along file (longitude), or two squares along rank (latitude) and one square along file (longitude). The knight is the only piece that can leap over other pieces. It moves the same way when capture an opponent’s piece.
 |
| Knight's move and capture on the Dot |
Pawn: The pawn may move forward (approach to opponent’s pole) to the unoccupied square immediately in front of it on the same file (longitude), or on its first move it may advance two squares along the same file (longitude) provided both squares are unoccupied. The pawn may not move backwards (away from opponent’s pole).
The pawn may capture an opponent’s piece on a square diagonally in front (approach to opponent’s pole) of it on an adjacent file (longitude), by moving to that square. The pawn may not move to these squares if they are vacant.
|
| Pawn's capture on the Dot |
Castling: This consists of moving the king two squares along the “polar circle” toward a rook and then placing the rook on the last square the king has just crossed.
 |
| Castling on the Dot |
En passant: A special pawn capture which can occur immediately after a player makes a double-step move from its starting position, and an opponent’s pawn could have captured it had the pawn moved only one square forward (approach to opponent’s pole).
 |
| En passant on the Dot |
Promotion: The transformation of a pawn that reaches its opponent’s “polar circle” into the player’s choice of a queen, knight, rook, or bishop of the same color. Every pawn that reaches its eighth rank (opponent’s polar circle) must be promoted.
 |
| Promotion on the Dot |
To sun up, the only difference between “Chess” and “Chess on the Dot ” is the topological shape of the chessboard. A chess player can play “Chess on the Dot” without learning any new rules.
The End